A evolução das coordenadas

René Descartes e Pierre de Fermat

A matemática é uma ciência de cunho exato, mas que, de acordo com as palavras do meu brilhante professor Michael Souza, é muitos mais sentimental do que simplesmente exata. De toda forma as abstrações precisam ser representadas muitas vezes em planos. O usina mostrará os sistemas de reprodução gráfica em planos: As coordenadas fermatianas (injustamente chamadas de cartesianas), as coordenadas polares, cilíndricas e esféricas. As três ultimas partem de modificações em formas de escrever a primeira e possuem uma simples modificação em relação ao plano fermatiano. Outras coordenadas, menos conhecidas são usadas: coordenadas elípticas, parabólicas, hiperbólicas.

Cartesiano? Não! Fermatiano.

Pra começo de conversa a relação entre René Descartes e Pierre de Fermat era horrível, eles competiam sempre de maneira rigorosa, mas pra evidenciar os fatos foi René que começou a briga (dá pra imaginar o Fermat correndo e dizendo: ele que começou mãe, eu só me defendi), de fato Fermat respondia sempre com um nível de calma impressionante, O nome Cartesiano vem de Cartesius e é a forma latinizada de Descartes. Acontece que foi fermat o pioneiro a trabalhar com eixos perpendiculares a descoberta das equações da reta e da circunferência, e as equações mais simples de elipses, parábolas e hipérboles. Uma menção honrosa foi o fato de que ao cometer o erro com cálculos diferenciais e integrais, René terminou com a equação x³ +y³ - 3axy = 0 e, mesmo sem saber a resposta, desafiou Pierre a representar a reta tangente da equação no plano cartesiano (embora fosse o plano do próprio fermat), a surpresa foi que Fermat representou a equação sem grandes dificuldades e batizou seu gráfico de folium de descartes (folium significa folha).

folium de descartes

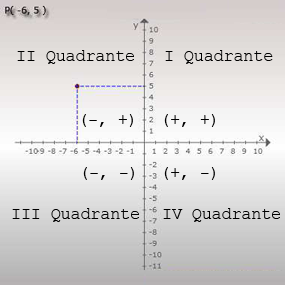
O plano.

Contamos com o eixo X (chamado de abscissas) e o eixo Y (as ordenadas). Por meio de funções das duas variáveis podemos, representar um ponto X associado a outro(s) Y(s), os pontos (x,y) são chamados de pares ordenados. Além disso, os eixos tem comprimentos infinitos e no final o plano é uma grande cruz imensurável que divide a dimensão (plano) em quatro. Cada parte é então chamada de Quadrante. Da forma que os quadrantes variam de sinal para números acima de zero (positivo) e abaixo de zero (negativo). A reta X é horizontal com variação de menor numero a maior da esquerda para direita, e a de Y é vertical com variação de baixo para cima. Os pontos representados são tais que:

Coordenadas Polares

Não, nada de pensar em urso polar, ou em frio (Ba dum tss).

Desenvolvido pelo pai da probabilidade Jacques Bernoulli, o sistema se baseia em um único eixo, chamado de eixo polar. Os pontos são construídos através de um tamanho r que representa a reta (coordenada radial) e um ângulo teta que representa a angulação frente ao eixo polar (ângulo polar ou azimute). Desta vez o plano é o Euclidiano (Espaço euclidiano é um espaço vetorial real de dimensão finita munido de um produto interno).

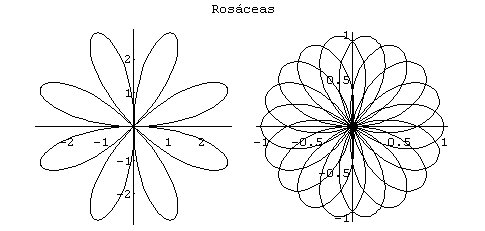
Através dele, podemos desenhar figuras que expressem conceitos não abordados na coordenada fermatiana figuras como:

             Limaçons (coração)                           Lemniscatas (infinito)

              Rosáceas (flores)                                       Espirais

A terceira dimensão

Até aqui, tudo foi visto com a interpretação de x e y, uma análise de pontos bidimensional, entretanto para a melhor compreensão dos próximos sistemas é necessário incluir uma dimensão a mais, a terceira dimensão, ou o segmento z. A direção de z é complicada de falar, mas seria para cima, o eixo y agora toma a posição do eixo x enquanto o x se manifesta indo a sua direção, mais ou menos como se uma reta saísse da tela em direção a você. O eixo z acaba fazendo uma divisão nova nos quadrantes e originando novos planos. Estes se chamam Octantes, a área de cada plano é denominada de plano ab, onde ab são os segmentos que formam o plano. O plano mais importante para estudarmos as próximas coordenadas é o plano xy ou yx.

         

Mais ou menos isso aqui.

Coordenadas cilíndricas.

As coordenadas cilíndricas são um aprimoramento das coordenadas polares, colocando-as uma dimensão acima, os pontos agora que nos interessam são denominados de ρ (Rô), φ (fi) e z. ρ representa o comprimento de reta traçado no plano xy, φ representa um ângulo de deslocamento partindo de x e indo de encontro a y, finalmente, z representa a distância do ponto real em relação ao plano xy.

 Fonte Ebah.

As coordenadas cilíndricas são de grande contribuição para facilitar o cálculo diferencial e infinitesimal.

Coordenadas esféricas.

As últimas coordenadas abordadas são as esféricas, confesso que foi a que eu menos estudei  no curso de cálculo III e possui um grau de dificuldade mais acentuado (devido a não interesse tão forte).  A ideia aqui é representar um ponto em um espaço de formato esférico. Na realidade a mudança é um tanto quanto baseada na cilíndrica, o sistema usa três dimensões (do plano xyz) e envolve três parâmetros:  r (um comprimento de raio, similar ao ρ, mas em espaço tridimensional), ϴ, um ângulo que a decomposição de r forma em relação ao plano xy, e ϕ (fi minúsculo) que é o ângulo que a reta r se situa em relação ao eixo yz). O espaço pode ser visto como um conjunto de esferas concêntricas, onde o raio serve como delimitador máximo da superfície de cada esfera e os ângulos determinam a localização exata dos pontos sobre a superfície. Observe que graficamente r varia de zero a infinito, ϴ pode admitir toda a volta trigonométrica (0 a 2π) e ϕ vale meia volta (0 a π).

 Existem ainda outras coordenadas que não são tão usadas quanto essas. E grande parte do publico deve conhecer apenas a primeira, porém a polar é uma quebra no conceito e com ela, a cilíndrica e a esférica aparecem, completando o seu sentido.

Se angulo é um parâmetro importante em grande parte das coordenadas, saibam que existe uma conversão trigonmétrica

De polares a conversão para fermatiana é:

 

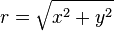
De cilíndricas a conversão fermatiana é:

As esféricas são mais complexas em todos os conceitos:

Seja como for, o sistema de coordenadas que tinha o intuito de apresentar apenas a explanação de uma ideia, consegue agora materializar quase todo pensamento geométrico.